As part of my participation in the Iron Viz 2020, I created a new type of visualisation using Tableau, which has received a lot of positive feedback. I called it ‘isometric hexmap’. In this article, I explain how to reproduce this type of representation and give you access to the source files. You can access the interactive version on Tableau Public.
If you like this visualisation, feel free to leave a comment and to use it.
The principle of the isometric hexmap
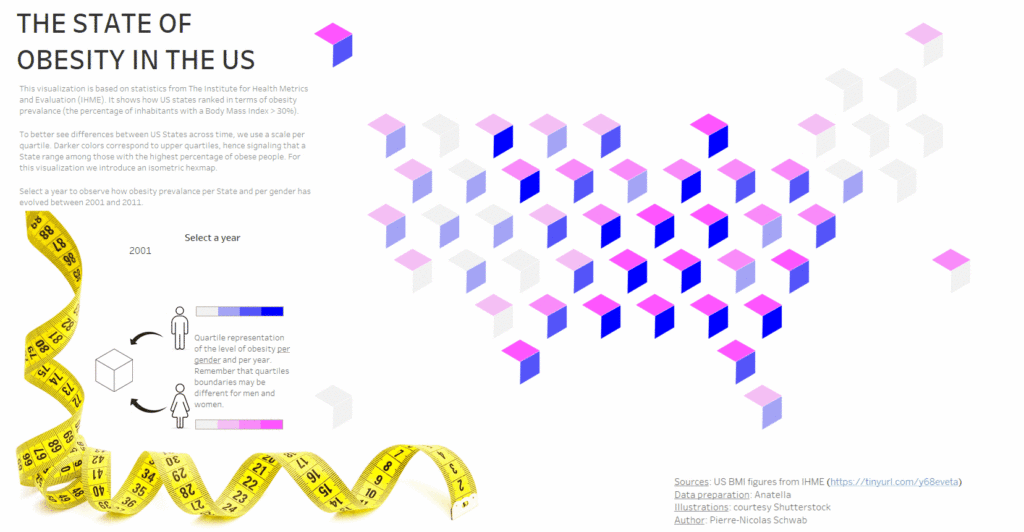
The visualisation represents the levels of obesity in the states of the United States. The levels are expressed as quartiles to show the differences from year to year better. A cube is used to represent male obesity on one side and female obesity on the other. The illusion of the cube in 3D is obtained thanks to lozenges imitating each face; a white face is left free.
This isometric visualisation derives from the classic hexmap and therefore requires a grid of coordinates (x,y) for the different elements to be placed.
Data origin and data preparation
Data on obesity in the United States come from the IHME. To avoid a join in Tableau, I have chosen to enrich the database with the “hexmap” coordinates (column, row) beforehand in Anatella. I have already talked about this great ETL.
A step by step guide for creating an isometric hexmap
To help you, I have created a small video (see below; I’ll add the sound as soon as I have time) that you’ll find above. The creation of the isometric hexmap is straightforward. However, it requires that you download the 2 specific png files that you will have to copy in the “shapes” folder of Tableau. These particular shapes create an isometric effect. You can download the 2 files here and here.
You will also need a specific file with the x and y coordinates of the points you wish to place. I have prepared a file (downloadable here) in which I have compiled different ways of representing the American states: either with the coordinates on a hexmap or via their centroids.
Finally, the most “complicated” part will consist of preparing the quartile representation, which will allow to appreciate the differences year after year. The procedure derives from the one proposed here. The principle is to distribute the states in a quartile for each year according to the proportion of obese people in the male and female population.
- Data pivoting
- Creating a “quantile” parameter
The parameter is an integer with a minimum value of 1 and a maximum value of 4. The default value must be 4. - Creation of a calculated variable “obesity” for each gender
if CONTAINS([gender],"male")=true then ([obesity value]) else NULL end - Creation of a LOD expression for obesity per year
{FIXED [Year],[State] : AVG([obesity value female])} - Calculation of the rank
RANK_PERCENTILE(AVG([obesity US states male])) - Creation of a calculated variable for colour by quartile
if [rank percentile obesity female]<=1/[quantile]
then 1/[quantile]
ELSEIF [rank percentile obesity female]<=2/[quantile]
then 2/[quantile]
ELSEIF [rank percentile obesity female]<=3/[quantile]
then 3/[quantile]
ELSEIF [rank percentile obesity female]<=4/[quantile]
then 4/[quantile]
END - Displaying the points of the hexmap
The display is done very simply by passing the reference points in the fields “column” on the one hand, and “line” on the other. Don’t forget to enter the variables as “dimension” otherwise you will display the sum of points. - Assignment of shapes
Once the two png files are downloaded, copy them to your table folder in the “shapes” directory. Then change the type of shape to use one diamond for category 1 (male obesity in my case) and the other diamond for category 2 (female obesity in my case).
- Assignment of colours
The assignment of colours is done there as well simply by using the variable created in step 7. Use a colour gradient limited to the number of quantiles (in my case 4).
and there you go!
The result
To see the result, you can either go to my Tableau Public profile (don’t forget to bookmark it in your favourites) or watch the animated gif below.
I invite you to think about other applications that are possible with the use of isometric shapes. Feel free to share your findings and thoughts as comments.
Posted in big data.